আমাদের চারপাশে অনেক ধরনের গতি রয়েছে। একজন যখন সাইকেল চালিয়ে যায় সেটি একধরনের গতি, যখন একটি গাড়ি যায় সেটিও একধরনের গতি। যখন প্লেন উড়ে যায় সেটিও গতি, পৃথিবী যখন সূর্যের চারদিকে ঘুরে সেটিও একটি গতি। ঝুলন্ত একটি বাতি যখন দুলতে থাকে সেটিও গতি, রাইফেল থেকে যখন বুলেট বের হয় সেটিও গতি। আপাতদৃষ্টিতে মনে হয় এই নানা ধরনের গতি বুঝি সব ভিন্ন ভিন্ন ধরনের গতি, কিন্তু তোমরা জেনে খুবই অবাক এবং খুশি হবে যে একেবারে অল্প কয়েকটি রাশি দিয়ে এই সবগুলোকে ব্যাখ্যা করা সম্ভব। এই অধ্যায়ে সেই রাশিগুলো, তাদের একক, মাত্রা এবং একের সাথে অন্যের কী সম্পর্ক সেগুলো আলোচনা করা হবে। 

আমাদের চারপাশে যা কিছু আছে তার মাঝে কোনটি স্থির বা স্থিতিশীল এবং কোনটি চলমান বা গতিশীল সেটি বুঝতে আমাদের কখনো অসুবিধা হয় না। আমাদের চোখ দিয়ে আমরা এমনভাবে দেখি যে, কোনো কিছু একটুখানি নড়লেই আমরা চট করে সেটা ধরে ফেলতে পারি। কাজেই স্থিতি বা গতি বলতে কী বোঝায় সেটি আমরা খুব চমৎকারভাবে অনুভব করতে পারি। কিন্তু পদার্থবিজ্ঞানের জন্য শুধু অনুভব করা যথেষ্ট নয়, সেটাকে ভালোভাবে সংজ্ঞায়িত করতে হয়। সেটি করার জন্য আমরা এক কথায় বলতে পারি যে, সময়ের সাথে কোনো কিছুর অবস্থানের যদি পরিবর্তন না হয় তাহলে সেটি স্থির, আর যদি অবস্থানের পরিবর্তন হয় তাহলে সেটি গতিশীল। 

এখন আমাদের ‘অবস্থান' শব্দটির ভালো করে ব্যাখ্যা করা দরকার। আমাদের দৈনন্দিন কথাবার্তায় আমরা নানাভাবে অবস্থান শব্দটি ব্যবহার করলেও পদার্থবিজ্ঞানের ভাষায় অবস্থান শব্দটির একটি সুনির্দিষ্ট অর্থ রয়েছে। যেমন তোমাকে যদি জিজ্ঞেস করা হয় তোমার স্কুলের অবস্থান কোথায় এবং তুমি যদি উত্তর দাও ‘ঝিলটুলি'তে তাহলে উত্তরটি সঠিক হলেও স্কুলের অবস্থানটি কিন্তু জানা গেল না। তুমি যদি উত্তর দাও, তোমার স্কুলটি তোমার বাসার গেট থেকে এক কিলোমিটার দূরে, তাহলেও কিন্তু স্কুলের অবস্থান জানা গেল না। তোমার বাসার গেটটি কোথায় সেটি আমাদের জানা থাকলেও আমরা বলতে পারব না স্কুলটি সেখান থেকে ঠিক কোন দিকে এক কিলোমিটার দূরে। কিন্তু তুমি যদি বলো স্কুলটি তোমার বাসার গেট থেকে পূর্ব দিকে এক কিলোমিটার দূরে তাহলেই শুধু আমরা সুনির্দিষ্টভাবে তোমার স্কুলের অবস্থানটি জানতে পারব। অর্থাৎ স্কুলের অবস্থান জানার জন্য দূরত্ব এবং দিক দুটিই সুনির্দিষ্টভাবে জানতে হয়। শুধু তাই নয়, সেই দূরত্ব এবং দিকটি নির্দেশ করতে হয় একটি নির্দিষ্ট বিন্দু বা প্রসঙ্গ বিন্দুর অবস্থান থেকে। তোমার স্কুলের বেলায় প্রসঙ্গ বিন্দু (origin) ছিল তোমার বাসার গেট। সেটি তোমার বাসার গেট না হয়ে একটা বাস স্টপ কিংবা একটা শপিং মল হতে পারত। তাহলে অবশ্যই দূরত্ব এবং দিকটির ভিন্ন মান হতো কিন্তু অবস্থানটি অবশ্যই এই নতুন প্রসঙ্গ বিন্দুর সাপেক্ষে বলে দিতে পারতাম। অর্থাৎ কোনো কিছুর অবস্থান বলতে হলে সেটি বলতে হয় কোনো একটি প্রসঙ্গ বিন্দুর সাপেক্ষে। এই প্রসঙ্গ বিন্দুটি চূড়ান্ত কোনো বিষয় নয়, আমরা আমাদের সুবিধা অনুযায়ী যেকোনো বিন্দুকে প্রসঙ্গ বিন্দু বা মূল বিন্দু হিসেবে ধরতে পারি। 

এখন প্রশ্ন হচ্ছে অবস্থান নির্দিষ্ট করার জন্য আমাদের যে প্রসঙ্গ বিন্দু বা মূল বিন্দু ধরে নিতে হয় সেই বিন্দুটি কি স্থির একটি বিন্দু হওয়া প্রয়োজন? ধরা যাক তোমার সামনে আরেকজন চেয়ারে স্থির হয়ে বসে আছে। তোমার চেয়ারটাকে যদি প্রসঙ্গ বা মূল বিন্দু ধরে নিই তাহলে নিশ্চিতভাবে বলা যেতে পারে তোমার বন্ধুর অবস্থানের কোনো পরিবর্তন হচ্ছে না।কিন্তু যদি এমন হয় তোমরা আসলে চলন্ত একটি ট্রেনে বসে আছ তাহলে কী হবে? ট্রেনের বাইরে স্টেশনে দাঁড়িয়ে থাকা একজন মানুষ বলবে, তুমি কিংবা তোমার বন্ধু দুজনেই গতিশীল, কেউ স্থির নয়! তাহলে কার কথাটি সত্যি? তোমার, নাকি স্টেশনে দাঁড়িয়ে থাকা মানুষটির? আসলে তোমার কিংবা স্টেশনে দাঁড়িয়ে থাকা মানুষটির, দুজনের কথাই সত্যি! তার কারণ মূল বিন্দু বা প্রসঙ্গ বিন্দু যদি সমবেগে চলতে থাকে তাহলে আমরা কখনোই জোর দিয়ে বলতে পারব না যে প্রসঙ্গ বিন্দুটি কি সমবেগে চলছে নাকি এটা আসলে স্থির এবং অন্য সবকিছু উল্টো দিকে সমবেগে চলছে! কাজেই আমরা বলতে পারি যদি কোনো একটি মূল বিন্দুর সাপেক্ষে কোনো বস্তুর অবস্থানের পরিবর্তন হয় তাহলে সেই বস্তুটি ঐ বিন্দুর সাপেক্ষে গতিশীল। মূল বিন্দুটি কি আসলে স্থির নাকি সমবেগে চলছে সেটি নিয়ে আমরা মাথা ঘামাব না। সেটি গুরুত্বপূর্ণ নয়, তার কারণ সব গতিই আপেক্ষিক। 

শুধু তাই নয়, আমরা যদি সত্যিকারের স্থির কোনো একটি প্রসঙ্গ বিন্দু খুঁজে বেড়াই তাহলে বিপদে পড়ে যাব। পৃথিবীর পৃষ্ঠে কোনো কিছুকে মূল বিন্দু ধরে নিলে একজন আপত্তি করে বলতে পারে পৃথিবী তো স্থির নয় সেটা নিজের অক্ষের উপর ঘুরছে কাজেই পৃথিবী পৃষ্ঠের সবকিছু ঘুরছে। আমরা বুদ্ধি করে বলতে পারি পৃথিবীর কেন্দ্র হচ্ছে মূল বিন্দু। তখন আরেকজন আপত্তি করে বলতে পারে যে সেটিও স্থির নয়, সেটি সূর্যের চারদিকে ঘুরছে। আমরা তখন আরো বুদ্ধি খরচ করে বলতে পারি সূর্যের কেন্দ্রবিন্দুটিই হোক মূল বিন্দু! তখন অন্য কেউ আপত্তি করে বলতেই পারে সূর্যও তো স্থির নয়, সেটাও তো আমাদের গ্যালাক্সির (বাংলায় নামটি ছায়াপথ, ইংরেজিতে Milky Way) কেন্দ্রকে ঘিরে ঘুরছে। বুঝতেই পারছ তখন কেউ আর সাহস করে গ্যালাক্সির কেন্দ্রকে মূল বিন্দু বলবে না! গ্যালাক্সি বিশ্বব্রহ্মাণ্ড স্থির কে বলেছে? শুধু তাই নয়, গ্যালাক্সির কেন্দ্রবিন্দুকে মূল বিন্দু ধরা হলে পৃথিবী পৃষ্ঠের একটা অবস্থান বর্ণনা করতে আমরা কী পরিমাণ জটিলতায় পড়ে যাব কেউ চিন্তা করেছ? 

আসলে এত জটিলতার কোনো প্রয়োজন নেই, আমাদের কাজ চালানোর জন্য আমাদের কাছে স্থির মনে হয় এরকম যেকোনো বিন্দুকে মূল বিন্দু ধরে সব কাজ করে ফেলতে পারব, শুধু বলে নিতে হবে সব মাপজোখ এই মূল বিন্দুর সাপেক্ষে করা হয়েছে। বিজ্ঞানীরা এভাবে পরমাণুর ভেতরে নিউক্লিয়াস থেকে শুরু করে মহাকাশে পাঠানো উপগ্রহ সবকিছুর মাপজোখ করে ফেলতে পারেন, কখনো কোনো সমস্যা হয়নি! 

আমরা আমাদের চারপাশে অনেক রকম গতি দেখতে পাই, কোনো কিছু নড়ছে, কোনো কিছু কাঁপছে, কোনো কিছু ঘুরছে, কোনো কিছু সরে যাচ্ছে—এই সবই হচ্ছে নানা রকম গতির উদাহরণ। সম্ভাব্য গতির কোনো শেষ নেই কিন্তু আমরা ইচ্ছে করলে কিছু কিছু গুরুত্বপূর্ণ গতির কথা আলাদা করে বলতে পারি। 

• সরলরৈখিক গতি (Linear Motion ): এটি সবচেয়ে সহজ গতির উদাহরণ। কোনো কিছু যদি সরলরেখায় যায় তাহলে তার গতিটি হচ্ছে সরলরৈখিক গতি। কোনো কিছুকে সমঙ্গলপৃষ্ঠে থাকা দিয়ে ছেড়ে দিলে সেটা সরলরেখায় যেতে থাকে। একটা বলকে উপর থেকে ছেড়ে দিলে সেটা সোজা নিচের দিকে পড়ে, কাজেই সেটাও রৈখিক গতি । 
• ঘূর্ণন গতি (Circular Motion): কোনো কিছু যদি একটা নির্দিষ্ট বিন্দুর সমদুরত্বে থেকে ঘুরতে থাকে তাহলে সেটাকে বলে ঘূর্ণন গতি। বৈদ্যুতিক পাখা, ঘড়ির কাঁটা এগুলো ঘূর্ণন গতির উদাহরণ হলেও চমকপ্রদ একটা উদাহরণ হচ্ছে আকাশের চাঁদ। চাঁদকে কোনো কিছু দিয়ে পৃথিবীর সাথে বেঁধে রাখা নেই ভৰু এটা পৃথিবীকে ঘিরে ঘুরছে, শুধু তাই নয়, এটা টুপ করে পৃথিবীতে পড়েও যাচ্ছে না! 
• চলন গতি (Translational Motion): কোনো কিছু যদি এমনভাবে চলতে থাকে যেন বস্তুর সকল কণা একই সময় একই দিকে যেতে থাকে তাহলে সেটা হচ্ছে চলন গতি। আমরা আমাদের চারপাশে মাঝে মাঝে এরকম অনেক উদাহরণ দেখতে পাই। কোনো কিছু যখন সোজা (রৈখিক গতি বার তখন তার উদাহরণ দেখা খুব সহজ। গাড়ির ঘূর্ণায়মান ঢাকা বিবেচনায় না আনলে সোজা এগিয়ে যাওয়া একটা গাড়ি চলন গতির উদাহরণ, তখন গাড়ির প্রতিটি বিন্দু একই সময় একই দিকে একই দূরত্ব অতিক্রম করছে।চলন গতি সোজা হতেই হবে এমন কোনো বাধ্যবাধকতা নেই কিন্তু আঁকাবাঁকা পথে চলন গতির উদাহরণ সহজে পাওয়া যাবে না।  

• পর্যায়বৃত্ত গতি (Periodic Motion ): কোনো গতিশীল বস্তু যদি নির্দিষ্ট সময় পর পর একটি নির্দিষ্ট বিন্দু দিয়ে একই দিকে একইভাবে অতিক্রম করে তাহলে সেটাকে পর্যায়বৃত্ত গতি বলা যায়। আমাদের হৃৎপিন্ডের স্পন্দন পর্যায়বৃত্ত কারণ সেটি নির্দিষ্ট সময় পর পর একইভাবে একই দিকে স্পন্দিত বা গতিশীল হয়। পর্যায়বৃত্ত গতি বৃত্তাকার (ফ্যানের পাখা), উপবৃত্তাকার (সূর্যকে ঘিরে হ্যালির ধূমকেতুর কক্ষপথ), কিংবা সরলরৈখিক (স্প্রিংয়ে ঝুলিয়ে রাখা দুলতে থাকা কন্তু) হতে পারে। ঘূর্ণন গতি একটি বিশেষ ধরনের পর্যায়বৃত্ত গতি।
•  
• সরল স্পন্দন গতি (Simple Harmonic Motion) :একটি বিশেষ ধরনের পর্যায়বৃত্ত পতি হচ্ছে সরল স্পন্দন গতি। স্পন্দন গতির বেলার একটি নির্দিষ্ট বিন্দুর দুই পাশে বস্তুটি স্পন্দিত হয়। বস্তুটি একেবারে স্থির অবস্থা থেকে শুরু করে ধীরে ধীরে গতিশীল হয়। কেন্দ্রবিন্দুতে সর্বোচ্চ গতিতে পৌঁছায় তখন এর গতি কমতে থাকে। গতি কমতে কমতে এটি এক সময় থেমে যায় তখন এটি গতিপথ পরিবর্তন করে বিপরীত দিকে গতিশীল হয় । বিপরীত দিকে সর্বোচ্চ গতিশীল হওয়ার পর আবার এর গতি কমতে থাকে, এক সময় পুরোপুরি থেমে আবার আগের দিকে ধীরে ধীরে গতিশীল হয় এবং এভাবে চলতেই থাকে।
•  আমাদের চারপাশে স্পন্দন গতির অসংখ্য উদাহরণ রয়েছে। স্প্রিং থেকে দুলিয়ে দেওয়া একটা বস্তুর গতি হচ্ছে স্পন্দন গতি। দোলনায় দুলতে থাকা শিশু কিংবা ঘড়ির পেন্ডুলাম এর উদাহরণ। আমরা যখন কথা বলি তখন বাতাসের অণু এই গতি দিয়ে শব্দকে সামনে এগিয়ে নিয়ে যায়। আমরা এতক্ষণ বিশেষ কয়েক ধরনের গতির কথা বলেছি, কিন্তু এই গতিগুলোর কারণটি কোথাও বলিনি। পদার্থবিজ্ঞানের সবচেয়ে বড় সাফল্য হচ্ছে যে, এটি শুধু যে বস্তুর বিচিত্র গতির কারণটি খুঁজে বের করবে তা নয় এর গতিটি সুনির্দিষ্টভাবে ব্যাখ্যা করতে পারবে।                                                                                                                           তুমি কি গতির কারনটি অনুমান করতে পারবে?

আমাদের পরিচিত জগতে আমরা যা কিছু পরিমাপ করতে পারি সেটাই রাশি—আনন্দ কিংবা দুঃখ রাশি নয় কিন্তু তাপমাত্রা রাশি। তার কারণ আনন্দ কিংবা দুঃখকে মেপে একটা মান দেওয়া যায় না কিন্তু তাপমাত্রা মেপে মান দেওয়া সম্ভব। তোমার শরীরের তাপমাত্রা 37° C কিংবা 98.4°F । তাপমাত্রা বোঝানোর জন্য একটি সংখ্যা বললেই চলে কিন্তু অনেক রাশি আছে, যেগুলোকে একটি সংখ্যা দিয়ে পুরোপুরি প্রকাশ করা যায় না, হয় তার মানের সাথে একটা দিক বলে দিতে হয়, কিংবা একাধিক মান বলে দিতে হয় যেন সেগুলো মিলিয়ে তার মান এবং দিক দুটোই নির্দিষ্ট করে দেওয়া যায়। অবস্থান ছিল সে রকম একটি রাশি, সেটা বোঝানোর জন্য আমাদের শুধু দূরত্ব দিয়ে কাজ হয়নি, তার দিকটিও নির্দেশ করতে হয়েছিল! কাজেই যে রাশি শুধু একটি সংখ্যা দিয়ে প্রকাশ করা যায় সেটা হচ্ছে ফেলার আর যেটা প্রকাশ করার জন্য একটা দিকও বলে দিতে হয়, সেটা হচ্ছে ভেক্টর। 

তাপমাত্রা ছাড়াও স্কেলারের উদাহরণ হচ্ছে সময়, দৈর্ঘ্য কিংবা ভর। কারণ এগুলো শুধু একটা সংখ্যা দিয়ে প্রকাশ করে ফেলা যায়। তোমরা দেখবে অবস্থান ছাড়াও ভেক্টরের উদাহরণ হচ্ছে বেগ কিংবা বল। তোমাদের পরের অধ্যায়েই এই বেগ এবং বলের সাথে পরিচয় করিয়ে দেওয়া হবে। কারণ এগুলো প্রকাশ করতে হলে মানের সাথে সাথে দিকটাও বলে দিতে হয়। 

ভেক্টর রাশিকে স্কেলার রাশি থেকে আলাদা করে লেখার জন্য সেটাকে মোটা (Bold) করে লেখা হয় (x, y কিংবা A, B )। বইয়ে কিংবা কম্পিউটারে প্রিন্ট করার সময় যেকোনো কিছু মোটা করে লেখা সহজ। কিন্তু যখন কেউ হাতে কাগজে লিখে তখন কোনো কিছুকে ভেক্টর বোঝানোর জন্য তার উপরে ছোট করে একটা তাঁর চিহ্ন দেওয়া হয়  ( $\overrightarrow{x,}\overrightarrow{y}$কিংবা $\overrightarrow{A},\overrightarrow{B}$) । 

তোমাদের এখানে যেটুকু পদার্থবিজ্ঞান শেখানো হবে সেখানে আসলে সত্যিকার অর্থে ভেক্টরের ব্যবহারের প্রয়োজন হবে না, বড়জোর কোনটা স্কেলার কোনটা ভেক্টর মাঝে মাঝে সেটা মনে করিয়ে দেওয়া হবে। 

আমরা দূরত্ব শব্দটির সাথে খুব ভালোভাবে পরিচিত, তবে সরণ (displacement) শব্দটি দৈনন্দিন কথাবার্তায় সেভাবে ব্যবহার করি না। আমরা একটি উদাহরণ দিয়ে দূরত্ব এবং সরল শব্দ দুটির মাঝে সম্পর্কটি বোঝার চেষ্টা করি। 2.01 চিত্রে একটি আঁকাবাঁকা রাস্তা দেখানো হয়েছে। এই রাস্তাটিতে A বিন্দুর সাপেক্ষে রাস্তার অতিক্রান্ত দূরত্বগুলো কিলোমিটারে 1, 2, 3 সংখ্যা দিয়ে দেখানো হয়েছে। 

ধরা যাক তুমি A বিন্দুতে আছ, (অর্থাৎ তোমার অবস্থান A বিন্দু) এখন তুমি সাইকেল চালিয়ে আঁকাবাঁকা পথটি ধরে 4 km রাস্তা অতিক্রম করে B বিন্দুতে পৌঁছেছ। আমরা বলতে পারব A এবং B বিন্দুর ভেতরকার দূরত্ব 4 km । দুরত্ব একটি স্কেলার রাশি, কাজেই A এবং B বিন্দুর ভেতরকার দূরত্ব বোঝানোর জন্য কোনো দিকের কথা বলে দিতে হবে না। 

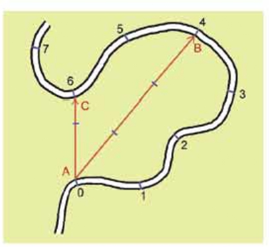
    চিত্র 2.01: A বিন্দু থেকে শুরু করে আঁকাবাঁকা পথে সাইকেল যাওয়া

A বিন্দুর সাপেক্ষে B বিন্দুর "সরণ" বের করতে আমরা A বিন্দুর সাপেক্ষে এই পথটি ধরে B বিন্দুর দূরত্ব” বের করেছি। এখন ইচ্ছে করলে পারি। সরণ বলতে বোঝানো হয় A বিষ্ণুর অবস্থানের সাপেক্ষে B বিন্দুর অবস্থান। ছবিতে A বিন্দু থেকে B বিন্দু পর্যন্ত একটা তীর চিহ্নিত সরলরেখা দিয়ে সরণটি দেখানো হয়েছে। এই ছবিতে সরণের মান 3 km এবং তীরের দিকটি হচ্ছে সরণের দিক। অর্থাৎ সরণ হচ্ছে ভেক্টর রাশি, এর মান এবং দিক দুটিই আছে। 

যদি তুমি সাইকেল দিয়ে আরো দুই কিলোমিটার অতিক্রম করে মোট হয় কিলোমিটার পথ অতিক্রম করে C বিন্দুতে পৌঁছাও তোমার সরণ হবে তীর চিহ্নিত সরলরেখা AC, যার মান 1.5 কিলোমিটার এবং এখানেও তীরের দিকটি তোমার সরণের দিক। যদিও তুমি আঁকাবাঁকা পথ ধরে বেশি দূরত্ব অতিক্রম করেছ কিন্তু সরণ হয়েছে কমা অর্থাৎ বেশি দূরত্ব অতিক্রম করলেই বেশি সরণ হবে সেটি সত্যি নয়। শুরু থেকে শেষ অবস্থানের পার্থক্য হচ্ছে সরণ। 

A থেকে শুরু করে আঁকাবাঁকা পথে B পর্যন্ত দূরত্ব 4 km ঠিক একইভাবে B থেকে A পর্যন্ত হচ্ছে 4 km, দুটোই সমান। কিন্তু লক্ষ করে দেখো A থেকে B পর্যন্ত সরণ আর B থেকে A পর্যন্ত সরণ কিন্তু সমান নয়। একটি আরেকটির নিগেটিভ বা ঋণাত্মক। ভেক্টর হিসেবে লিখতে পারি : 

                                             $\overrightarrow{AB}=-\overrightarrow{BA}$

দূরত্ব কিংবা সরণ, দুটোর মাত্রাই হলো দৈর্ঘ্যের মাত্রা। 

                                      [সরণ] = L (ভেক্টর )

                                      [দূরত্ব] = L (স্কেলার )

বেগ বলতে কী বোঝানো হয় আমরা সবাই সেটা মোটামুটি জানি। কোনো কিছু কত দ্রুত যাচ্ছে তার পরিমাপটা হচ্ছে বেগ। তবে পদার্থবিজ্ঞানের ভাষায় বেগের একটা সুনির্দিষ্ট অর্থ আছে এবং বেগের পাশাপাশি আমরা দ্রুতি (speed) নামে আরো একটা রাশি ব্যবহার করি। আমরা যদি দূরত্ব এবং সরণ এই বিষয় দুটো ভালোভাবে বুঝে থাকি তাহলে দ্রুতি এবং বেগ এই রাশি দুটোও খুব সহজে বুঝতে পারব। 

দ্রুতি হচ্ছে সময়ের সাথে দূরত্বের পরিবর্তনের হার। 

অর্থাৎ তুমি যদি 20 সেকেন্ডে 100 m দূরত্ব অতিক্রম করে থাকো তাহলে তোমার দ্রুতি v হচ্ছে: 

                                                 $v=\frac{100 m}{20 s}=5 m/s$

দ্রুতির মাত্রা  

বেগ হচ্ছে সময়ের সাথে সরণের পরিবর্তনের হার।  

অর্থাৎ যদি 20 সেকেন্ডে কোনো নির্দিষ্ট দিকে তোমার অবস্থানের পরিবর্তন হয় 50m তাহলে তোমার বেগের মান হচ্ছে:

                                           $v=\frac{50 m}{20 s}=2.5 m/s$

বেগ যেহেতু ভেক্টর তাই তার দিকটি নির্দিষ্ট করে দিতে হবে। 

বেগের মাত্রা: 

এখানে একটা বিষয় লক্ষ করা যেতে পারে, আমরা যদি শুধু রৈখিক গতি বিবেচনা করি তাহলে বেগ আর দ্রুতির মাঝে কোনো পার্থক্য নেই, বেগের মানটিই হচ্ছে দ্রুতি। তোমাদের এই বইয়ে আমরা শুধু রৈখিক গতিই বিবেচনা করব তাই দ্রুতি এবং বেগের মাঝে পার্থক্য খুঁজে পাব না। তাই দ্রুতি এবং বেগের ভেতরকার সম্পর্ক বোঝানোর জন্য রৈখিক গতির বাইরে কয়েকটা উদাহরণ নেওয়া যাক:  

2.01 চিত্রে আমরা দূরত্ব এবং সরণ বোঝানোর জন্য একটি আঁকাবাঁকা রাস্তা এবং সেখানে ভিন্ন ভিন্ন অবস্থান দেখিয়েছি। দ্রুতি এবং বেগ বোঝানোর জন্য আমরা সেই একই উদাহরণ নিতে পারি তবে এবারে কতটুকু সময়ে তুমি একটি অবস্থান থেকে অন্য অবস্থানে গিয়েছ সেটি বলে দিতে হবে। ধরা যাক সাইকেলে A থেকে B অবস্থানে আসতে তোমার সময় লেগেছে 20 minutes. তাহলে তোমার গড় দ্রুতি হচ্ছে: 

                               গড় দ্রুতি = অতিক্রান্ত দূরত্ব / সময় 

অর্থাৎ, 

                       $v=\frac{4 km}{20 minutes}=\frac{4\times 1000 m}{20\times 60 s}=3.33 m/s$

এখানে লক্ষ করো আমরা দ্রুতি শব্দটি ব্যবহার না করে গড় দ্রুতি শব্দটি ব্যবহার করেছি। কারণ তুমি সাইকেল চালানোর সময় হয়তো কখনো একটু জোরে কখনো একটু আস্তে সাইকেল চালিয়েছ। তাই “তাৎক্ষণিক” দ্রুতি আমরা বলতে পারব না, 20 minutes সময়টুকুর গড় দ্রুতিটুকুই শুধু বলতে পারব। 

এবারে আমরা বেগ বের করার চেষ্টা করি। দ্রুতির মতোই আমরা কিন্তু তাৎক্ষণিক বেগ বের করতে পারব না, এই পুরো সময়টিতে তুমি ভিন্ন ভিন্ন বেগে সাইকেল চালিয়েছ। গতি বেশি কিংবা কম হওয়ার কারণে বেগের পরিবর্তন হয়েছে আবার দিক পরিবর্তন হওয়ার কারণেও বেগের পরিবর্তন হয়েছে। এই সবগুলো পরিবর্তন মিলিয়ে গড় বেগের মান হচ্ছে: 

                                     গড় বেগ = সরণ / সময় 

অর্থাৎ, 

                      $v=\frac{3 km}{20 minutes}=\frac{3\times 1000 m}{20\times 60 s}=2.5 m/s$

তোমরা দেখতে পাচ্ছ এই উদাহরণটিতে গড় দ্রুতির মান থেকে গড় বেগের মান কম। পথটি যদি আঁকাবাঁকা না হয়ে সোজা হতো তাহলে গড় বেগের মান আর গড় দ্রুতি দুটোই সমান হতো। আমাদের এই উদাহরণে তুমি যদি সব সময় একই গতিতে সাইকেল চালিয়ে যেতে তাহলে আমরা বলতাম তুমি সুষম দ্রুতিতে সাইকেল চালিয়ে এসেছ। যখন কোনো কিছু সুষম দ্রুতিতে যায় তখন তার তাৎক্ষণিক দ্রুতি এবং গড় দ্রুতির মান একই হয়ে যায়। 

লক্ষ করো, পথটি যেহেতু আঁকাবাঁকা ভাই এই পথে গেলে ক্রমাগত তোমার দিক পরিবর্তন হচ্ছে, তাই এই পথে তুমি সুষম দ্রুতিতে পেলেও সুষম বেগে যেতে পারবে না। শুধু রৈখিক গতিতে সরলরেখায় গেলেই সুষম বেগে কিংবা সমবেগে বাওয়া সম্ভব ।

যখন কোনো বস্তু সমবেগে যায় তখন তার কোনো ত্বরণ নেই। বেগের পরিবর্তন হলেই বুঝতে হবে সেখানে স্বরণ রয়েছে। আরো সুস্পষ্ট করে বললে বলতে হবে ত্বরণ হচ্ছে সময়ের সাথে বেগের পরিবর্তনের হার। 

বেগের যেহেতু দিক এবং মান দুটিই আছে তাই বেগের পরিবর্তন দুভাবেই হতে পারে। আমাদের আগের উদাহরণে তুমি যখন আঁকাবাঁকা পথে সাইকেল চালিয়ে গিয়েছ, তখন যতবার তুমি বাঁক নিয়েছ ততবার তোমার বেগের পরিবর্তন হয়েছে অর্থাৎ তোমার ত্বরণ হয়েছে। তুমি পুরো পথটুকু সম্প্রতিতে গিয়ে থাকলেও শুধু দিক পরিবর্তনের জন্য ত্বরণ হয়েছে। তুমি যদি আগের উদাহরণের মতো একটা পাথরকে সুতা দিয়ে বেঁধে মাথার উপর সশ্রুতিতে ঘোরাতে থাক তাহলে ঘুরতে থাকা পাথরটির ক্রমাগত দিক পরিবর্তন হবে। অর্থাৎ তার বেগের পরিবর্তন হবে বা স্বরণ হবে। 

যদি তোমার গতি সরলরৈখিক হয়ে থাকে তাহলে দিক পরিবর্তনের কোনো সুযোগ নেই। তার স্বরণ হতে পারে শুধু বেগের মানের (দ্রুতি) পরিবর্তনের কারণে। যদি বেগের মান বাড়তে থাকে তাহলে আমরা বলি বেগের দিকে বস্তুটির ত্বরণ হচ্ছে। যদি বেগের মান কমতে থাকে আমরা বলি বস্তুটির ঋণাত্মক ত্বরণ বা মন্দন হচ্ছে। আমরা এখন সরলরেখায় চলমান কোনো একটি বস্তুর ত্বরণ বের করতে পারি। 

এই অধ্যায়ে আমরা শুধু রৈখিক গতি নিয়ে আলোচনা করব, অর্থাৎ যদি বেগের মানের পরিবর্তন হয় শুধু তাহলেই ত্বরণ হবে। 

ত্বরণ হচ্ছে বেগের পরিবর্তনের হার, যদি সমত্বরণ হয়, অর্থাৎ সময়ের সাথে সাথে ত্বরণের পরিবর্তন না হয় তাহলে আমরা লিখতে পারি: 

                                 ত্বরণ=(শেষবেগ−আদিবেগ)/সময়

অর্থাৎ যদি প্রথমে কোনো কিছুর বেগ হয় u এবং t সময় পর তার বেগ হয় v ,  তাহলে ত্বরণ a হচ্ছে, 

                                                       $a=\frac{v-u}{t}$

ত্বরণের মাত্রা

ত্বরণের একক $m{s}^{-2}$

কাজেই যদি ত্বরণ জানা থাকে তাহলে কোনো বস্তুর আদি বেগ u হলে t সময় পর তার বেগ v বের করা খুব সোজা।  

                                                           v = u + at 

বস্তুটি যদি স্থির অবস্থা থেকে শুরু করে তাহলে 

                                                               v= at 

আমরা ইতিমধ্যে বলেছি এখন পর্যন্ত যা বলা হয়েছে তার সবকিছু সত্যি সমত্বরণের জন্য। যদি সমত্বরণ না হয় তাহলে কিন্তু এত সহজে শুধু আদি বেগ আর শেষ বেগ থেকে ত্বরণ বের করে ফেলা যাবে না। 

আমরা আমাদের চারপাশে গতির যেসব উদাহরণ দেখি, গাড়ি, ট্রেন বা সাইকেলের গতি তাদের ত্বরণ প্রায় সব সময়ই অসম ত্বরণ। যেমন একটি গাড়ি যদি স্থির অবস্থা থেকে শুরু করে ধীরে ধীরে বেগবান হয় তাহলে তার  ত্বরণ শূন্য থেকে শুরু করে ধীরে ধীরে একটি মানে পৌঁছায়, গাড়ি যখন তার পূর্ণ বেগে পৌঁছায় তখন তার গতি আর বাড়ে না অর্থাৎ ত্বরণ আবার শূন্য হয়ে যায়, আবার গাড়িটি যদি বেগ কমিয়ে থামতে শুরু করে তাহলে মন্দন হতে থাকে। গাড়িটি যদি পুরোপুরি থেমে যায় । 

তাহলে তার বেগ এবং ত্বরণ দুটিই শূন্য হয়ে যায়। তোমাদের মনে হতে পারে সমত্বরণের উদাহরণ খুঁজে পাওয়া বুঝি খুব কঠিন। 

আসলে আমরা আমাদের চারপাশে যা কিছু দেখি তার মাঝে কিন্তু সমত্বরণের খুব চমকপ্রদ একটা উদাহরণ আছে। সেটি হচ্ছে মাধ্যাকর্ষণজনিত ত্বরণ (g)। পৃথিবীপৃষ্ঠের কাছাকাছি তার মান $9.8 m{s}^{-2}$ আমরা যদি কোনো একটা বস্তু স্থির অবস্থা থেকে ছেড়ে দিই তাহলে দেখতে পাই তার গতিবেগ v = gt হিসেবে বাড়তে থাকে। 

আমরা যেহেতু শুধু রৈখিক গতি নিয়ে আলোচনা করব তাই গতি সম্পর্কে আলোচনা করতে গিয়ে আমরা এখন পর্যন্ত যে যে রাশিগুলোর কথা বলেছি সেগুলো হচ্ছে: 

u: আদি বেগ, সময়ের শুরুতে যে বেগ 

a: ত্বরণ 

t: যে সময়টুকু অতিক্রান্ত হয়েছে 

v: অতিক্রান্ত সময়ের পর বেগ  

s: অতিক্রান্ত সময়ে যে দূরত্ব অতিক্রম করেছে। 

অর্থাৎ, এই রাশিগুলোর কখনোই দিকের পরিবর্তন হবে না। অর্থাৎ আমরা এগুলোকে ভেক্টর হিসেবে বিবেচনা না করে শুধু এগুলোর মান নিয়ে আলোচনা করা হলেই কাজ চলে যাবে।

এই রাশিগুলোর মাঝে যে সম্পর্ক রয়েছে তার প্রায় সবগুলো এর মাঝে আমরা বের করে ফেলেছি, শুধু একটি বাকি রয়ে গেছে সেটি হচ্ছে s বা অতিক্রান্ত দূরত্ব। যদি কোনো ত্বরণ না থাকে তাহলে বেগের পরিবর্তন হয় না তাই আদি বেগ আর শেষ বেগ সমান (u=v) আর অতিক্রান্ত দূরত্ব হচ্ছে  

                                                    s =vt 

যদি সমত্বরণ থাকে তাহলে 

                                                v = u + at 

যার অর্থ সময়ের সাথে সাথে বেগের পরিবর্তন হচ্ছে। কাজেই অতিক্রান্ত দূরত্ব বের করতে হলে প্রতি মুহূর্তের বেগের সাথে সেই মুহূর্তের সময় গুণ করে পুরো সময়ের জন্য হিসাব করতে হবে। এই ধরনের হিসাব-নিকাশ করার জন্য বিশেষ গণিত (ক্যালকুলাস) জানতে হয়, আমরা সেগুলো ছাড়াই কাজটা করে ফেলব। সেটা সম্ভব হবে কারণ আমরা শুধু সমত্বরণ নিয়ে মাথা ঘামাচ্ছি। সমত্বরণ না হলে এটি সম্ভব হতো না। 

প্রতি মুহূর্তে বেগের পরিবর্তন হচ্ছে তাই আমরা s = vt লিখতে পারছি না কিন্তু আমরা যদি একটা গড় বেগ V ধরে নিই তাহলে কিন্তু লিখতে পারতাম 

                                                  s = Vt 

তার অর্থ অতিক্রান্ত দূরত্ব বের করার জন্য আমাদের শুধু গড় বেগটি বের করতে হবে । সমত্বরণের জন্য বিষয়টি সহজ। কোনো কিছু যদি সমহারে বাড়তে থাকে তাহলে তার গড় মান হচ্ছে 

 ঠিক মাঝামাঝি সময়ের মান। অন্যভাবে বলা যায় যদি কোনো কিছু সমহারে বাড়তে থাকে তাহলে শুরু এবং শেষ মানের পড় হচ্ছে গড় মান। 

অর্থাৎ 

                            কাজেই অতিক্রান্ত দূরত্ব 

                                               s=Vt 

                                            $s=\left(u+\frac{1}{2}at\right)t$

                                          $s=ut+\frac{1}{2}a{t}^2$

এখন পর্যন্ত আমরা পতির যে সমীকরণগুলো বের করেছি তার প্রত্যেকটিতেই সময় বা আছে। আমরা ইচ্ছে করলে এই সমীকরণগুলো ব্যবহার করে একটা সমীকরণ বের করতে পারি যেখানে t নেই। যেমন: 

  এই সমীকরণটি অন্য একটি সাধারণ সমীকরণের মতো দেখলেও এর মাঝে কিছু চমকপ্রদ পদার্থবিজ্ঞান লুকিয়ে আছে, যেটি আমরা চতুর্থ অধ্যায়ে তোমাদের দেখাব। 

আমরা বলেছি যে সমত্বরণের একটি চমকপ্রদ উদাহরণ হচ্ছে মাধ্যাকর্ষণজনিত ত্বরণ g, এর প্রভাবে যেকোনো বস্তু উপর থেকে ছেড়ে দিলে এটি গতিশীল হয়ে নিচের দিকে নামতে থাকে। এ ধরনের পড়ন্ত বস্তু দেখে গ্যালিলিও তিনটি সূত্র বের করেন। সূত্রগুলো স্থির অবস্থা থেকে মুক্তভাবে পড়তে থাকা বস্তুর বেলায় ব্যবহার করা যায়। সূত্রগুলো হচ্ছে:  

প্রথম সূত্র: স্থির অবস্থান ও একই উচ্চতা থেকে বিনা বাধায় পড়ন্ত বস্তু সমান সময়ে সমান পথ অতিক্রম করবে। 

দ্বিতীয় সূত্র: স্থির অবস্থান থেকে বিনা বাধায় পড়ন্ত বস্তুর নির্দিষ্ট সময়ে (t) প্রাপ্ত বেগ (v) ঐ সময়ের সমানুপাতিক। অর্থাৎ $v\propto t$

তৃতীয় সূত্র: স্থির অবস্থান থেকে বিনা বাধায় পড়ন্ত বস্তু নির্দিষ্ট সময়ে যে দূরত্ব (h) অতিক্রম করে তা সময়ের (t) বর্গের সমানুপাতিক। অর্থাৎ $h\propto t^2$

আমরা সমত্বরণের উদাহরণ হিসেবে g বা মাধ্যাকর্ষণজনিত ত্বরণের কথা বলেছিলাম। গতি সম্পর্কে আমরা যে সমীকরণগুলো বের করেছি সেগুলোকে খুব সহজেই আমরা পড়ন্ত বস্তুর গতি ব্যবহার করার জন্য বের করতে পারি। অতিক্রান্ত দূরত্বের বেলায় s ব্যবহার করা হয়েছিল, এবারে উচ্চতা বোঝানোর জন্য h ব্যবহার করব, ত্বরণের জন্য a না লিখে g লিখব , শুধু এ দুটোই হবে পার্থক্য

গ্যালিলিওর পড়ন্ত বস্তুর যে তিনটি সূত্র আছে সেগুলো আসলে এই সূত্রগুলো ছাড়া আর কিছু নয়। 

প্রথম সূত্রটি বলছে যে একই উচ্চতা থেকে ছেড়ে দেওয়া হলে যেকোনো বস্তু একই সময়ে নিচে পড়বে অর্থাৎ এটি বস্তুর ভরের উপর নির্ভর করবে না। এটি আমাদের দৈনন্দিন জীবনের অভিজ্ঞতার সাথে খাপ খায় না। এক টুকরো কাগজ আর একটি ছোট পাথর উপর থেকে ছেড়ে দিলে আমরা দেখি পাথরটি আগে এবং কাগজটি পরে নিচে এসে পড়ে। এটি ঘটে বাতাসের বাধার কারণে, বাতাসহীন একটি টিউবে এরকম পরীক্ষা করা হলে কাগজ এবং পাথর একই সময়ে নিচে এসে পড়ত। পড়ন্ত বস্তুর সূত্রগুলো থেকে গ্যালিলিওর প্রথম সুত্রটি বোঝা যায়। তার কারণ পড়ন্ত বস্তুর বেগ বা অতিক্রান্ত উচ্চতার সমীকরণগুলোতে কোথাও বস্তুর ভর নেই, অর্থাৎ ভারী এবং হালকা সব বস্তুর উপরেই মাধ্যাকর্ষণজনিত ত্বরণ সমানভাবে কাজ করে। কাজেই সমান সময়ে বেগ এবং অতিক্রান্ত দূরত্ব সমান। 

গ্যালিলিওর দ্বিতীয় সূত্রটি g এর কারণে বেগ বৃদ্ধির সূত্র। আদি বেগ u শূন্য হলে বেগ v এর সাথে সমানুপাতিক। গ্যালিলিও এর তৃতীয় সূত্রটি অতিক্রান্ত উচ্চতা h এর সূত্রটি ছাড়া আর কিছু নয়। এই সূত্রটিতে u = 0 ধরে নেওয়া হলে আমরা দেখতে পাই অতিক্রান্ত উচ্চতা t2 এর সমানুপাতিক।